Een internationaal perspectief op reken- en wiskundeonderwijs, nr. 5
Bert Zwaneveld, Wiskunde voor Morgen
In de internationale literatuur op het gebied van het reken- en wiskundeonderwijs staat het specifieke karakter van rekenen en wiskunde centraal. Deze literatuur laat zien dat dit vak heel specifieke eisen stelt aan het onderwijs. In deze reeks wil de werkgroep Wiskunde voor Morgen dit internationale perspectief voor het voetlicht brengen aan de hand van toonaangevende internationale artikelen.
De basis voor deze bijdrage aan de reeks Een internationaal perspectief op reken- en wiskundeonderwijs is te vinden in drie van Schoenfelds artikelen: Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (1992), Reflections on Problem Solving Theory and Practice (2013), en Reframing Teacher Knowledge: a research and development agenda (2020).
Globaal gesproken is Schoenfelds boodschap dat het in het reken- en wiskundeonderwijs gaat om het wiskundig denken dat leerlingen zich eigen moeten maken, en niet om het oefenen van allerlei vaardigheden die – heden ten dage – net zo goed of zelfs beter aan technische hulpmiddelen overgelaten kunnen worden.
In het artikel van 1992 geeft Schoenfeld zijn visie op wat wiskunde inhoudt, en op wat als een gevolg daarvan het doel van reken- en wiskundeonderwijs is: wiskundig denken en wiskundig probleemoplossen. In het artikel van 2013 laat Schoenfeld niet alleen zien wat zijn kader voor wiskundig probleemoplossen is, maar ook dat dit kader inmiddels als een theorie voor probleemoplossen in het algemeen kan worden beschouwd, en dus niet beperkt is tot wiskundig probleemoplossen. Schoenfeld spreekt daarbij van á la minute besluiten nemen in een complexe zaak, in kennisintensieve, hoog-sociale omgevingen. Schoenfeld gaat daarbij in op wat de consequenties zijn voor het opzetten van de wiskundelessen op school. In het artikel van 2020 geeft Schoenfeld aan op welke terreinen er vervolgontwikkelingen en onderzoek zullen moeten plaats vinden.
Wiskunde en wiskundig denken: het artikel van 1992
In dit artikel geeft Schoenfeld zijn visie op wiskunde en wiskundeonderwijs (in mijn vertaling):
Wiskunde is een inherent sociale activiteit, waarin een gemeenschap van getrainde beoefenaren, wiskundige wetenschappers, zich bezig houden met het doorzien van patronen, dat wil zeggen het bestuderen van en experimenteren met patronen door activiteiten als systematisch proberen gebaseerd op waarnemingen. Het doel is de kern van de reguleringsprincipes van een patroon te bepalen en die vast te leggen in axiomatische of theoretische (‘zuivere wiskunde’) systemen, dan wel in de vorm van modellen van systemen, waarbij geabstraheerd is van objecten in de reële wereld (‘toegepaste wiskunde’). De werktuigen of hulpmiddelen van de wiskundige zijn abstractie, symbolische weergave en symbolische manipulatie. Het gebruiken van deze hulpmiddelen door een getrainde wiskundige, is vergelijkbaar met het gebruiken van werktuigen door iemand die zich daarmee als vakman kwalificeert. Leren wiskundig te denken betekent (a) het ontwikkelen van een wiskundig kijk op de processen van mathematisering, het waarderen van abstractie en het hebben van voorliefde om deze te gebruiken, en (b) het ontwikkelen van de competentie deze hulpmiddelen te gebruiken om een structuur te begrijpen, en daarmee aan wiskunde betekenis te geven.
Schoenfeld gaat verder met de constatering dat iedereen die met iets nieuws geconfronteerd wordt begint met ‘gissen’ wat er aan de hand is. Hij gebruikt de term ‘to guess’. Dat gissen kan verkeerd uitpakken, zodat men iets anders probeert. Op een gegeven moment heeft men (enigszins) zekerheid en gaat men redeneren. In de wiskunde betekent dat wat met proberen begint over kan gaan in bewijzen. “Als het leren van wiskunde iets, wat dan ook, met wiskunde te maken heeft, dan moet de leerling de mogelijkheid krijgen aan het werk te gaan met problemen waarbij eerst iets ‘gegist’ wordt en dat daarna bewezen wordt op een voor de leerling passend niveau.” Over dat gissen merkt Schoenfeld op dat een leek dit ‘eerst gissen daarna beslissen’ helemaal niet vreemd vindt, die doet dat zelf ook. Van een natuurwetenschapper wordt dit zelfs verwacht, in de vorm van experimenteren. Dat ook een wiskundige aan dit gissen doet is voor een leek op zijn minst een verrassing.
Wat in de vorige alinea wordt beschreven staat in schril contrast met de algemene opvatting dat wiskunde sterk verbonden is met zekerheid: iets weten en dan het juiste antwoord geven. Deze culturele aanname komt voort uit schoolervaringen. Op school betekent immers wiskunde doen het volgen van de regels zoals de docent die heeft geformuleerd; en wiskunde weten betekent het herinneren en toepassen van de juiste regel als de docent een vraag stelt. De wiskundige waarheid is vastgesteld als de docent het antwoord goedkeurt. Een gevolg van deze vorm van wiskundeonderwijs leidt tot een opvatting hoe wiskunde gedaan wordt en op school betekent dit dat wiskunde geleerd wordt door middel van jarenlang toekijken, luisteren en oefenen. Met andere woorden, op school draait het om: “exposition, examples, exercises” (uitleg, voorbeelden, oefeningen).
Wat betreft de inhoud van het wiskundeonderwijs is heden ten dage iedereen het er wel over eens dat er veel meer is dan alleen algebra en meetkunde; vroeger vormden die samen bijna de volledige wiskundige inhoud. Wiskunde is inmiddels een diverse discipline waarin het draait om data, metingen en waarnemingen, en waarbij het gaat om deductief redeneren en bewijzen, om het trekken van conclusies. Het ontwikkelen van, en werken met wiskundige modellen speelt een belangrijke rol: modellen van verschijnselen in de natuur, van menselijk gedrag en van sociale systemen.
Schoenfeld presenteert een lijst van lange-termijndoelen van wiskundeonderwijs. Wiskundeonderwijs moet:
- Leerlingen voorzien van een gevoel voor de discipline: bereik, kracht, gebruik en geschiedenis; hoe wiskunde werkt op een niveau dat is aangepast aan hun ervaringen en aan hun begrip; met als doel en hopelijk ook gevolg dat zij wiskunde waarderen en zich vertrouwd voelen bij hun wiskundige vaardigheden.
- Leerlingen ondersteunen een houding te ontwikkelen waarbij zij wiskundige objecten conceptueel begrijpen in plaats van mikken op mechanische vaardigheden.
- Leerlingen de mogelijkheid bieden een breed gebied van problemen en probleemsituaties te exploreren, door middel van opdrachten die lopen van oefeningen tot open problemen; daarbij wordt een breed scala van aanpakken en technieken aangeboden: rechtstreeks toepassen van algoritmische methoden, maar ook tot het gebruiken van benaderingsmethoden, modelleertechnieken en heuristische methoden. Op die heuristische methoden komen we terug.
- Leerlingen helpen een ‘wiskundige kijk’ te ontwikkelen: voorliefde voor analyseren en begrijpen te ontwikkelen, structuren en structurele verbanden te percipiëren, te zien hoe zaken in elkaar grijpen, analytische vaardigheden te ontwikkelen en te redeneren in een keten van argumenten.
- Leerlingen helpen nauwkeurigheid te ontwikkelen in schriftelijke en mondelinge presentaties voor de docenten en voor de medeleerlingen
- Leerlingen helpen de vaardigheid te ontwikkelen wiskundige teksten te lezen en te gebruiken, evenals andere wiskundige hulpmiddelen in te zetten. Kortom, leerlingen te leren zich te ontwikkelen tot onafhankelijke lerenden, vertolkers en gebruikers van zowel zuivere als toegepaste wiskunde.
In Schoenfelds opvatting moeten de wiskundige denkactiviteiten van leerlingen vergelijkbaar zijn met die van een wiskundige wetenschapper die, naar we kunnen verwachten, regelmatig bezig is met probleemoplossen. Bij zijn onderzoek naar probleemoplossen in de jaren tachtig speelden de door Pólya geformuleerde probleemaanpakken, ook heuristieken geheten, een belangrijke rol. Pólya’s heuristieken zijn manieren om problemen aan te pakken, zoals ‘bekijk een eenvoudiger geval’, ‘deel het probleem op in een aantal gevallen en probeer die op te lossen’, ‘bekijk een situatie met getallen in plaats van met variabelen’, enzovoorts. Ze kunnen helpen, maar garanderen geen succes. Schoenfeld heeft wel een nuancering bij Pólya’s heuristieken aangebracht: het zijn eerder klassen van mogelijke aanpakken die voor elke probleemsituatie opnieuw uitgewerkt moeten worden. Probleemoplossen, in de geest van Pólya, betekent worstelen met nieuwe, onbekende taken waarvan de relevante oplossingsmethoden niet bekend zijn, of hoogstens gedeeltelijk.
Schoenfeld noemt, naast het hebben van wiskundige kennis nog drie andere aspecten van probleemoplossen.
Het eerste is dat een oplosser moet leren zijn oplosproces te monitoren en zo nodig bij te stellen. Schoenfeld spreekt van ‘metacognitie’. Hij illustreert dit grafisch (zie figuur 1) met de probleemaanpak van een beginnende student bij een niet-standaardprobleem, met de probleemaanpak van een wiskundige bij een moeilijk probleem en met de probleemaanpak van twee studenten die expliciet getraind zijn in zichzelf te monitoren en het proces te reguleren. Zijn observaties zijn als volgt (in mijn vertaling). ‘Werkend aan complexe problemen, monitoren effectieve probleemoplossers de mate waarin ze vorderen, en dan bij hun aanpak blijven, dan wel aanpassen. Niet-succesvolle probleemoplossers neigen ernaar snel een oplossingsaanpak te kiezen en daaraan vast te houden, ondanks het feit dat ze geen vorderingen maken.’ Zwakke probleemoplossers blijven als het ware hangen in het proberen te doorgronden van het probleem. Hij presenteert drie aanpakken in de vorm van time-line grafieken. Zie de figuren 15.3, 15.4 en 15.5 in fig. 1. De pijltjes in de figuren 15.4 en 15.5 markeren de momenten waarop de probleemoplossers overlegden.
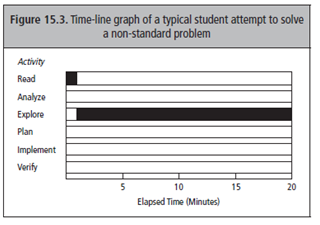
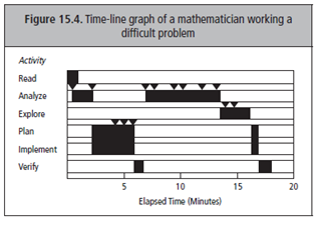
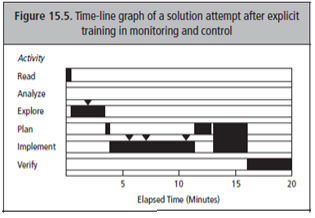
Over fig. 15.5 zegt Schoenfeld dat dit het best illustreert wat er gebeurt bij een tweetal studenten die zijn cursus ‘wiskundig denken en probleemoplossen’ hebben gevolgd. Na het lezen van het probleem sprongen ze naar een aanpak die helaas op verkeerde aannames was gebaseerd. Dit beseften ze een paar minuten later en ze probeerden een andere aanpak. Ook deze aanpak was niet goed, en ze raakten verstrikt in complexe berekeningen, die hen acht minuten bezig hield. Toen stopten ze opnieuw. Een van hen zei: “zo komen we nergens. … Laten we opnieuw beginnen en dit vergeten.” Dat deden ze en vonden de juiste oplossing.
Een derde aspect waaraan Schoenfeld aandacht besteedt zijn de opvattingen van studenten over probleemoplossen, ‘beliefs’ noemt hij ze. Typische opvattingen van studenten presenteert hij in fig. 2.

Bij probleemoplossen vervagen de grenzen tussen het cognitieve en affectieve domein: wiskundige kennis, metacognitie en opvattingen beïnvloeden elkaar. Schoenfeld onderscheidt problemen en oefeningen: bij oefeningen kan een leerling laten zien dat hij/zij een relatief klein begrippengebied beheerst. Hij vat dit als volgt samen, weer in mijn vertaling.
Samengevat, leerlingen die twaalf jaar reken-wiskundeonderwijs hebben gehad, hebben gewerkt aan duizenden ‘problemen’ die in feite oefeningen zijn. Men mag ervan uitgaan dat het werken aan zo’n ‘probleem’ niet meer dan een paar minuten heeft gekost. Dit leidt tot de opvatting dat een leerling die het materiaal heeft begrepen, de oefeningen kan maken. Iemand die dat niet lukt in een redelijke tijd begrijpt het materiaal dus niet: verkeerde conclusies bij de docent, onder andere dat leerlingen te snel opgeven, en frustratie bij de leerling.
Hij voegt eraan toe dat dit (in 1992 ) ook een veel voorkomende manier van toetsing is: met gestandaardiseerde meerkeuzevragen, meestal slechts betrekking hebben op minuscule delen van de vaardigheden en perspectieven die hier verstaan worden onder wiskundig denken.
(Wiskundige) problemen oplossen en beslissen a la minute: het artikel van 2013
In zijn artikel van 2013 reflecteert Schoenfeld opnieuw op (wiskundig) problemen oplossen. Hij begint met kort te herhalen van wat toen, in 2013, de stand was van zijn ‘kader voor het oplossen van wiskundige problemen’. Dit kader volgt hier in mijn vertaling. Het is in feite een samenvatting van wat hiervoor is beschreven.
De theoretische kern bestaat uit de volgende vier categorieën die noodzakelijk én voldoende zijn voor de analyse van het succes of stranden van iemands poging een probleem op te lossen:
- de kennis van het individu
- het gebruik door het individu van aanpakken voor probleemoplossen, bekend als heuristische aanpakken of heuristieken
- het monitoren en reguleren van het oplosproces door het individu (aspecten van metacognitie)
- de opvattingen van het individu over zichzelf, over wiskunde, over probleemoplossen, en de oorsprong van die opvattingen in de wiskundige ervaringen.
Schoenfeld gaat vervolgens in op de kern van wiskundeonderwijs: de leerlingen introduceren in wat de betekenis is van wiskunde. Dat betekent onder andere dat wiskunde niet het leren beheersen van wiskundige feiten en procedures is, maar dat het ook gaat om vragen stellen, problemen formuleren, en op een beredeneerde manier tot antwoorden komen. Kortom, wiskundig probleemoplossen is een onderdeel van betekenis geven aan wiskunde. Dat kan ertoe leiden dat ervaringen van leerlingen uit de wiskundeles ‘ontleerd’ moeten worden, bijvoorbeeld het idee dat het in de wiskunde gaat om het beheersen van feiten en procedures. Dat geldt ook voor opvattingen van leerlingen als ‘opgaven moeten in vijf minuten opgelost (kunnen) worden’, of ‘bewijzen hebben niets met ontdekken te maken’.
Hij stelt de vraag of niet al het wiskundeonderwijs op deze manier georganiseerd kan worden, ook een groot deel van bachelorprogramma’s, dus als ‘betekenis geven aan wiskunde, inclusief probleemoplossen’. Hij is ervan overtuigd dat dit kan, zonder verlies van inhoud. Schoenfeld verwijst naar het feit dat uit onderzoek blijkt dat de hoeveelheid tijd die leerlingen besteden aan het verklaren van hun ideeën de grootste impact op hun leren heeft. Maar dan moet de leeromgeving daar wel op ingericht zijn. Voor belangrijke aspecten van die leeromgeving kan bijvoorbeeld gedacht worden aan: de klas neemt actief deel aan explorerende gesprekken over betekenisvolle vragen, leerlingen worden gestimuleerd informatie te zoeken, daaraan argumenten te ontlenen en daarmee verklaringen op te stellen, leerlingen leren wat het betekent claims te leggen en dat de argumenten daarbij consistent zijn met de normen van het vak en dat er hulpmiddelen voor handen zijn voor de leerlingen.
Wiskunde onderwijzen: Teaching for Robust Understanding – 2020
In dit artikel introduceert Schoenfeld een nieuw kader dat zich richt op essentiële dimensies van de lespraktijk.
Hij geeft eerst zijn ideeën over docentenkennis: de verzameling van ’tacit and explicit’ percepties die de manieren sturen waarmee docenten gewoonlijk optreden. Hier hoort bij bewustzijn van niet alleen de context maar ook van interpersoonlijke relaties en de manieren waarop we situaties ‘lezen’ en daarop reageren. Onderzoek naar het nemen van beslissingen geven aan dat beslissingen á la minute van docenten functies zijn van hun kennis, hulpbronnen, oriëntaties, hun gevoel van wat er toe doet, en hun doelen. In een kader voor onderwijzen hoort dit allemaal een plaats te hebben. Hier een verkorte weergave van wat hij in 2013 schreef (in mijn vertaling).
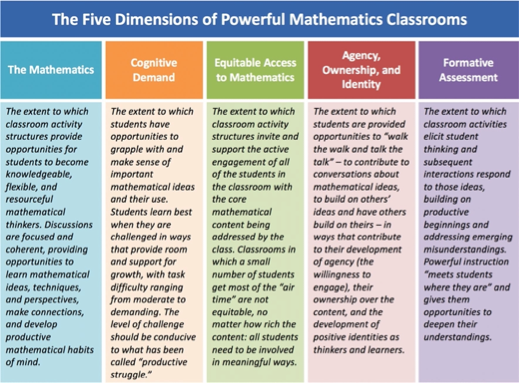
Als het over onderwijzen gaat, gaat het niet alleen over de docent, maar ook over de leerling, in ieder geval over de leeromgeving. De vragen zijn dan ook: waaraan moeten leeromgevingen voldoen waaruit leerlingen als krachtige denkers tevoorschijn komen, en welke docentenkennis hoort daarbij? Deze vragen staan centraal in het TRU-kader, een op onderzoek gebaseerd project, dat dergelijke leeromgevingen karakteriseert. Het TRU-kader benadrukt de mate waarin:
- De inhoud en praktijken waarin leerlingen worden ondergedompeld wiskundig rijk zijn.
- Leerlingen worden ondergedompeld in wiskunde betekenis geven en productief ‘worstelen’.
- Alle leerlingen evenzo worden ondergedompeld in de kerninhoud en kernpraktijken.
- De leeromgeving de leerlingen voorziet van mogelijkheden om met wiskunde zelf actie te ondernemen, eigenaarschap voor de wiskundige inhoud te nemen en een positieve wiskundige identiteit op te bouwen
- Formatief beoordelen doorlopend de mogelijkheid biedt de lespraktijk bij te stellen om de leerlingen to meet where they are.
In fig. 3 worden deze vijf dimensies van krachtige wiskundelespraktijken weergegeven. Uit een grote hoeveelheid van in de wetenschappelijke literatuur voorkomende aspecten van krachtige wiskundepraktijken zijn deze aspecten samengebald tot deze vijf dimensies.
Het TRU-kader is tot stand gekomen door heel veel video’s van lespraktijken te bestuderen en te scoren in rubrieken voor de docenten en de leerlingen. Voor de leerlingen gaat het vooral om de resultaten op toetsen van wiskundig denken en probleemoplossen.
Het TRU-kader heeft de volgende drie kenmerken. Ten eerste, de decompositie in vijf dimensies is niet uniek. Het is eerder zo dat ze de ‘onderwijsruimte’ opspannen. Het kan best zo zijn dat ook een andere verzameling basisvectoren mogelijk is. Zo is voorgesteld ‘de veiligheid in de klas bij een lessengesprek’ als essentieel te zien en dus als een aparte dimensie. In fig. 3 is dat niet als zodanig zichtbaar, maar het is wel aanwezig, je moet daarvoor deze tabel in zijn geheel bekijken. Dit is een gevolg van de keuze voor deze vijf basisvectoren als top, waarvan andere vectoren afhankelijk zijn. Veiligheid je te uiten in een klassengesprek heeft te maken met wiskundig acties ondernemen wat een serieus onderdeel van dimensie 4 is.
Ten tweede, in TRU verschuift het perspectief van ‘docent centraal’ naar ‘leerling centraal’: hoe voelt het onderwijs gezien vanuit de leerling? Dit perspectief wordt weergegeven in fig. 4.
Ten derde, TRU is niet voorschrijvend in de zin dat het voorschrijft hoe er onderwezen wordt, want er zijn veel verschillende goede manieren. Het gaat erom dat leerlingen in de gelegenheid worden gesteld om een gevoel van kunnen optreden, van eigenaarschap en identiteit te ontwikkelen (dimensie 4).

TRU onderwijs geven wordt geproblematiseerd door een serie vragen over de onderwijspraktijk te stellen. Bijvoorbeeld: hoe kan dat verbeterd worden (dimensie 1), hoe worden leerlingen ondersteund als ze vastlopen (dimensie 2), enzovoorts. TRU is niet in competitie met bestaande onderwijsbenaderingen, het kan gebruikt worden om die te problematiseren.
TRU is een oriëntatie op onderwijs dat de ervaringen van de leerlingen op de voorgrond stelt. Voor de docenten is nu de centrale vraag: over welke fundamentele begrippen en vaardigheden moet een docent beschikken om leeromgevingen te bouwen die krachtig zijn op elk van de vijf dimensies. Hoe kan deze docentenkennis worden vastgesteld en ondersteund worden?
Op basis van een heel lijstje van zijn internationale activiteiten en wetenschappelijke literatuur noemt Schoenfeld met betrekking tot wat essentiële wiskunde is voor de volgende generatie:
- de wiskundige inhoud: die zal blijven veranderen, denk hierbij aan data-analyse en modelleren
- de wiskundige praktijk: wiskundig modelleren, probleemoplossen, redeneren, zaken met elkaar verbinden, communiceren en redeneren worden steeds belangrijker.
Voorbeelden in het artikel van 2020
Schoenfeld geeft veel voorbeelden. Hier een kleine selectie.


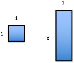
Fig. 7 About learning to work with variables
Afsluiting
We ronden af met een aantal conclusies van Schoenfeld. Hij noemt als eerste de uitdaging wiskunde op school te zien als een plek voor betekenis geven. Hij is ervan overtuigd dat alle wiskundige inhoud in basisschool en voortgezet onderwijs geïnterpreteerd kan worden als vormen van ‘patronen van betekenis geven’ wanneer leerlingen de juiste ervaringen worden gegeven; formele wiskunde kan worden gebruikt om deze ervaringen te organiseren en te systematiseren.
Ten tweede, de oriëntatie van docenten op wiskunde moeten gericht worden op wiskunde als een betekenis gevende discipline, waarbij leerlingen kunnen steunen op hun kennis en ervaringen buiten het klaslokaal, van waaruit ze kunnen leren om steeds krachtigere denkers en probleemoplossers te worden. Dit in een fundamenteel belangrijke component van docentenkennis.
Ten derde, docenten moeten ervoor zorgen dat de leerlingen zich in de leeromgeving zo veilig voelen dat ze hun ideeën durven uiten, goed luisteren naar ideeën van de medeleerlingen, en alle ideeën onderwerpen aan een kritische analyse en met ze doorgaan wanneer ze mogelijk en geschikt bevonden worden.
Over de erbij horende formatieve toetsing zegt Schoenfeld dat de belangrijkste functie ervan is het onderwijs en de leeractiviteiten aan te passen als daarmee aan de behoeften van de leerlingen tegemoet gekomen wordt. In fig. 8 wordt het verband tussen de formatieve toetsing en de andere vier dimensies van TRU weergegeven.
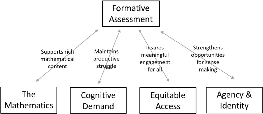
De vraag over de relaties tussen de vijf dimensies luidt in mijn vertaling: ‘
Welke soorten kennis, hulpmiddelen, oriëntaties en doelen zouden docenten in staat stellen leeromgevingen te bouwen die als rijk bestempeld worden, gelegd langs de vijf dimensies van TRU? Hoe kan deze kennis in de lerarenopleidingen ingebouwd worden?’
Er is weinig bekend hoe oriëntaties tot stand komen en hoe ze veranderen. Kennis hiervan is essentieel als we docenten willen ondersteunen in het ontwikkelen van oriëntaties die geschikt voor het hier beschreven onderwijs.
Kortom, er is nog veel onderzoek te doen, maar Schoenfeld zegt ervan overtuigd te zijn dat er een goede kans is tot een theoretisch volledige beschrijving te komen voor wat betreft de docentenkennis en hun beslissingen ten dienste van het creëren van wiskundig krachtige lessituaties.
Literatuur
Schoenfeld, A.H. (1992). Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics. Macmillan Publishing Co, Inc. Herdrukt in 2016: Journal of Education, 196(2).
Schoenfeld, A.H. (2013). Reflections on Problem Solving Theory and Practice. The Mathematics Enthusiast, 10(1).
Schoenfeld, A.H. (2016). Reframing teacher knowledge: a research and development agenda. ZDM, Mathematics Education, 52. 359-376.
