Een internationaal perspectief op reken- en wiskundeonderwijs Nr. 4

In de internationale literatuur op het gebied van het reken- en wiskundeonderwijs staat het specifieke karakter van rekenen en wiskunde centraal. Deze literatuur laat zien dat dit vak heel specifieke eisen stelt aan het onderwijs. In deze reeks wil de werkgroep Wiskunde voor Morgen dit internationale perspectief voor het voetlicht brengen aan de hand van toonaangevende internationale artikelen.

Koeno Gravemeijer en Frans van Galen, Werkgroep Wiskunde voor Morgen

In dit artikel richt Simon zich op de vraag, ‘Hoe kun je er als leraar voor zorgen dat de leerlingen de door jou beoogde wiskundige kennis en inzichten ontwikkelen, als je ervan uitgaat dat de leerlingen hun eigen kennis zelf construeren?’ Hij stelt deze vraag in de context van de opkomst van het (socio-)constructivisme. Zijn antwoord, waarin hij het denken van de leerlingen centraal stelt, is echter ook los van het constructivisme relevant voor het wiskundeonderwijs. 

We gebruiken het woord ‘wiskunde’ hier op dezelfde manier op als Simon, die het woord ‘mathematics’ ook gebruiken wanneer wij zouden spreken van ‘rekenen’ of ‘rekenen-wiskunde’. In dit artikel gaan we er steeds van uit dat ‘wiskunde’ ook het ‘rekenen’ omvat.

Inleiding

Simon constateert dat het constructivisme geen antwoord geeft op de vraag hoe je wiskunde moet onderwijzen. Constructivisme is een kentheorie, geen onderwijstheorie. Het constructivisme kan aanleiding zijn om leerlingen problemen te laten oplossen en daarover te laten discussiëren, maar het biedt géén voorschrift voor het onderwijzen van wiskunde. Volgens Simon kan constructivisme leraren wel helpen daarover na te denken. De leraren moeten zich verdiepen in de kennis en inzichten van de leerlingen en daar hun onderwijs op afstemmen. Hij verwijst hierbij naar Ball (1993), die opmerkt dat de leraren in twee richtingen moeten kijken, ze moeten vanuit het perspectief van de leerling naar de wiskunde kunnen kijken en vanuit het perspectief van wiskunde naar het denken van de leerling. 

Het socio-constructivisme geeft ook inzicht in wat het ‘didactisch contract’ wordt genoemd, het geheel van impliciete verwachtingen van leraren en leerlingen over elkaars rollen. In het traditionele onderwijs, waar voordoen-nadoen de norm is, is dat didactisch contract heel anders dan in onderwijs met een inquiry benadering. Daar is de norm dat de leerlingen zelf oplossingen bedenken en die ook moeten kunnen onderbouwen.

De vraag waar het Simon om gaat, is: ‘Hoe kunnen leraren leerlingen helpen wiskundige ideeën te construeren die wiskundigen in de loop van duizenden jaren ontwikkeld hebben?’ Simon probeert een antwoord op deze vraag te vinden door het uitvoeren van een onderwijsexperiment, waarin hij lesgeeft aan 26 studenten van een leraarsopleiding. Hij gaat daarbij uit van het idee van onderzoekend leren (inquiry-based). Zijn onderwijs kenmerkt zich door het oplossen van problemen in kleine groepjes en klassikale discussies over de oplossingen. Hij benadrukt dat de leraar hier een centrale rol heeft, onder verwijzing naar Richards (1991), die betoogt dat leerlingen niet zomaar actief gaan leren. Daar moet bewust naartoe worden gewerkt, met plannen die ontworpen zijn om verkennen en onderzoeken te stimuleren.

Opzet van deze samenvatting

Onze samenvatting van het artikel van Simon is als volgt opgezet. Na een korte introductie zoomen we in op onderwijsmodel dat Simon ontwikkelt op basis van een reflectie op zijn eigen rol in het onderwijsexperiment. Kernelementen in dit onderwijsmodel zijn de ‘mathematics teaching cycle’ en het ‘hypothetisch leertraject’.  Daarna beschrijven we het verloop van het onderwijsexperiment aan de hand van de cyclus, ontwerp, les, analyse, reflectie en herontwerp. Aansluitend op deze meer verhalende beschrijving vervolgen we met een beknopte samenvatting van het onderwijsexperiment in de vorm van opeenvolgende hypothetische leertrajecten en onderbouwingen. We sluiten af met een korte terugblik.

Het onderwijsmodel, Mathematics Teaching Cycle en Hypothetisch Leertraject

Het onderwijsexperiment omvatte acht lessen van 90 minuten, gegeven binnen een breder onderzoek rond multiplicatief redeneren. Het onderwerp betrof de wiskundige achtergrond van ‘oppervlakte = lengte x breedte’, de formule voor het berekenen van de oppervlakte van een rechthoek. Aanleiding voor het onderwijsexperiment was de constatering dat de oppervlakteformule voor de studenten een aangeleerde procedure leek, in plaats van te staan voor inzicht in de relatie tussen vermenigvuldigen en het meten van oppervlakte. Het doel van de lessen was om te proberen dit inzicht tot stand te brengen.

Simon beschrijft acht lessen. Het was nodig steeds weer nieuwe problemen aan de studenten voor te leggen, omdat de gegeven opdrachten niet tot het gewenste inzicht bleken te leiden. Het begon met een les waarin de studenten per groepje een kartonnen rechthoek kregen, met als opdracht om daarmee de oppervlakte van een tafeltje te meten. In een latere les kregen de studenten de figuur van hieronder, met de vraag hoe je van deze figuur de opdracht kunt bepalen.  

Uiteindelijk bleek een probleem rond het meten van oppervlakte met stokken heel bevorderlijk voor het inzicht van de studenten. Twee mensen – Louisa en Ruiz – meten een gebied op met stokken, maar hun stokken zijn niet even lang. 

Louisa zegt, ‘de lengte is vier van mijn stokken’. Ruiz zegt, ‘de breedte is vijf van mijn stokken’. Wat weten ze nu over de oppervlakte van dit gebied?

In feite is de vraag bij dit probleem hoe je een oppervlaktemaat kunt construeren gebaseerd op de lengte van de twee stokken.

Na de bespreking van het onderwijsmodel en het specifieke karakter van de onderwijsaanpak, beschrijven we de lessen in detail. Het artikel van Simon is vooral van belang door hoe hij beschrijft hoe hij na elk gegeven probleem reflecteert op wat het probleem opriep bij de studenten, en hoe hij vandaaruit weer een nieuw probleem koos. 

Terugkerend patroon

Terugblikkend op het geheel ziet Simon een patroon. Zijn analyse van het denken van de studenten vormt steeds startpunt voor het ontwerpen van de volgende opdracht. Dit brengt hem op het idee van wat hij een ‘mathematical teaching cycle’ noemt (figuur 3). Binnen deze wiskunde-onderwijs-cyclus, speelt het hypothetisch leertraject een centrale rol. Het hypothetisch leertraject bestaat uit drie componenten: het leerdoel waar je naartoe werkt, de leeractiviteiten en het hypothetische leerproces – ofwel een voorspelling over hoe het denken zal gaan verlopen. Anders gezegd, de leraar anticipeert op hoe de leerlingen, die met de beoogde activiteiten aan de slag gaan, zullen denken en vraagt zich af hoe dit denken bijdraagt aan het bereiken van de gekozen leerdoelen.  Simon wijst er daarbij op dat uitgevoerde onderwijsactiviteiten zullen verschillen van hoe ze bedacht waren, omdat ze veranderen door de manier waarop de leerlingen deze interpreteren en hoe de leraar daarop inspeelt.

Uiteraard kunnen de leerprocessen van individuele leerlingen verschillend verlopen. Simon veronderstelt echter dat er gemeenschappelijke patronen zijn, dat de manieren waarop de activiteiten worden geïnterpreteerd tot op zekere hoogte voorspelbaar zijn. Bovendien zal, denkt hij, een groot deel van de leerlingen in één klas kunnen profiteren van dezelfde opdracht. 

Waar het volgens hem omgaat, is, (1) dat de leraar met een hypothetisch leertraject een rationale heeft voor de keuzes die moeten worden gemaakt en (2) dat die rationale een hypothetisch karakter heeft. Die rationale en het hypothetisch leertraject worden steeds bijgesteld onder invloed van de ervaringen in de klas. Dat vormt de basis voor de mathematical teaching cycle (figuur 3).

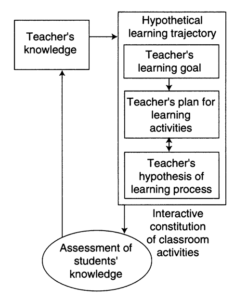
De cyclus verloopt als volgt. De kennis van de leraar vormt het startpunt. Op basis van deze kennis wordt het hypothetisch leertraject ontworpen. Daarna worden de onderwijsactiviteiten uitgevoerd. De leraar probeert vervolgens vast te stellen wat de leerlingen hiervan leren. Dit verandert/vergroot de kennis van de leraar. Op basis daarvan wordt het hypothetisch leertraject bijgesteld of opgevolgd door een nieuwe en start een nieuwe cyclus. Simon betoogt dat het ontwerp van het hypothetisch leertraject door tal van factoren wordt beïnvloed: de wiskundige kennis van de leraar, zijn/haar kennis van wiskundige activiteiten en -representaties, aannames over de kennis van de leerlingen, theorieën over het leren en onderwijzen van wiskunde, kennis over het leren van een specifieke wiskundige inhoud en de inschatting van de actuele kennis van de leerlingen. Hij werkt dit idee uit in een uitgebreider model, waarin deze invloeden in beeld worden gebracht (figuur 4).

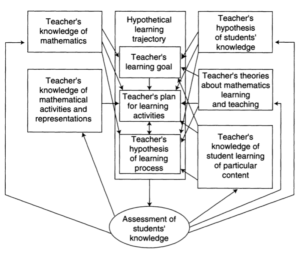
De mathematics teaching cycle vormt de motor van het onderwijs-leerproces, dat daarmee zorgt voor de kennisontwikkeling van de leerlingen. Maar niet alleen de kennis van de leerlingen groeit, ook de leraar ontwikkelt nieuwe kennis. Zowel kennis over leren en onderwijzen, als soms ook wiskundige kennis. Het denken over het behoud van oppervlakte is daar een voorbeeld van. Nog sterker komt dit naar voren in het bedenken hoe een oppervlaktemaat wordt bepaald door de maten waarmee de lengte en de breedte van een (grote) rechthoek worden gemeten. Wat Simon uitwerkt in het stokkenprobleem (figuur 2).

Het specifieke karakter van de onderwijsaanpak

Simon merkt op dat de lessenserie veel langer duurde dan was gepland. Dit heeft volgens hem te maken met het specifieke karakter van dit type onderwijs. Het idee was, dat het worstelen met problemen die een cognitief conflict zouden kunnen oproepen, de studenten zou helpen om diepere inzichten te ontwikkelen. Deze aanpak verschilt sterk van een meer traditionele aanpak. Daar wordt de leerstof in kleine stukjes opgedeeld, die één voor één worden aangeboden en systematisch worden geoefend. Omdat de stukjes zo klein zijn kunnen de leerlingen regelmatig successen boeken, zonder fundamentele inzichten te ontwikkelen. Simon hanteert een onderwijsvisie die ervan uitgaat dat de leerlingen leren van het overwinnen van conceptuele obstakels. In plaats van nog eens door te nemen wat oppervlakte inhoudt, of oefenopgaven aan te bieden, is de aanpak van Simon erop gericht een cognitief conflict op te roepen in de hoop het oplossen uitdaging hun inzicht in oppervlakte zouden vergroten. 

Hij merkt ten slotte op dat in de literatuur over de vernieuwing van het wiskundeonderwijs het belang van luisteren naar leerlingen en proberen hen begrijpen, veel aandacht krijgt. Maar het anticiperen op het leerproces van leerlingen veel minder. Van belang is naar zijn idee onderzoek naar hoe leerlingen bepaalde wiskundekennis (kunnen) ontwikkelen. Dat kunnen leraren gebruiken om te anticiperen op het denken van hun leerlingen. Simon werkt dit niet uit maar het ligt voor de hand om hier te denken aan ontwikkelingsonderzoek.

Hij sluit af met de constatering dat dit type onderwijs hoge eisen stelt. Om daaraan te voldoen moeten de leraren toegang hebben tot onderzoek over het denken van leerlingen, innovatieve curriculummaterialen en professionele support.

Beschrijving van het onderwijsexperiment

Simon gaat ervan uit dat de oppervlakteformule voor de studenten een aangeleerde procedure is en geen inzicht hebben in de relatie tussen oppervlakte en het vermenigvuldigen van lengtematen. Hij vermoedt dat ze nooit diep hebben nagedacht over wat er achter de bekende formule steekt. Hij ontwerpt daarom een opdracht waarmee hij wil proberen dit inzicht tot stand te brengen.

1 – Rechthoekenprobleem
Bepaal hoeveel rechthoeken, van de grootte en vorm van de kartonnen rechthoek dat je hebt gekregen, op het bovenoppervlak van je tafel passen. De rechthoeken mogen niet overlappen, niet worden geknipt en niet over de randen van de tafel steken. Bereid je voor om aan de klas uit te leggen hoe je dit probleem hebt opgelost.

Alle groepen gebruiken de kartonnen rechthoek om de lengte en de breedte van het tafelblad te meten om daarna de uitkomsten te vermenigvuldigden. Echter sommige groepen stellen de vraag of de kartonnen rechthoek steeds in dezelfde stand moet worden gehouden, of dat deze 90^o gedraaid moet worden, zodat je steeds met de lengte van de rechthoek meet (zie figuur 5b).

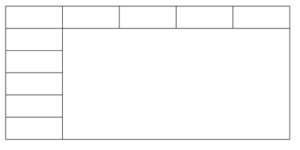
Tijdens het klassengesprek waarin de studenten hun oplossingen toelichtten stelt Simon de vraag waarom ze de getallen met elkaar hebben vermenigvuldigd. Hierop kwamen antwoorden als, ‘dat leek ons de eenvoudigste manier’, en, ‘we hebben deze formule in eerdere wiskundelessen geleerd’. Anderen zeggen dat het product hetzelfde is als het tellen van alle rechthoeken. Als Simon vraagt of ze kunnen uitleggen waarom dit altijd werkt, reageren de meeste studenten stomverbaasd. Eén van hen (Molly) komt echter wel met een toelichting. Zij wijst erop dat je bij vermenigvuldigen groepen optelt en dat je hier groepen maakt door te tellen hoeveel rechthoeken er op een rij passen. Dat je allemaal van zulke groepen kunt maken en dat je die bij elkaar kunt optellen door het aantal in een groep te vermenigvuldigen met het aantal groepen. Dat werkt altijd en komt op hetzelfde neer als het aantal langs de ene zijde vermenigvuldigen met het aantal langs de andere zijde. Molly licht dit toe met een bordtekening (zie figuur 6).

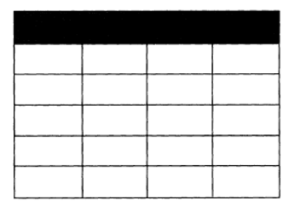
Uit de reacties van de andere studenten blijkt echter dat deze uitleg niet tot een wezenlijke verdieping van hun inzicht leidt.

Wanneer Simon hierop reflecteert constateert hij dat het niet zo was dat de anderen Molly’s uitleg niet konden volgen. Maar ze bleven op de vraag waarom je moet vermenigvuldigen reageren met, ‘dat hebben we zo geleerd,’ en ‘dat is een wiskundige wet.’ Hij komt tot de conclusie dat het vragen naar een onderbouwing (justification) niet werkt, omdat de studenten zich het idee van een wiskundige onderbouwing nog niet hebben eigen gemaakt. De hands-on activiteit had weliswaar tot discussie geleid, maar slechts enkele studenten hadden zich de beoogde wiskundige inzichten eigen gemaakt. 

Simon denkt dat er twee factoren zijn die een rol spelen. 1. De studenten gebruiken een procedure die weliswaar goed was geoefend, maar waar ze nooit inhoudelijk over hadden nagedacht. 2. Hun ideeën over waar het bij wiskunde omgaat, passen niet bij het redeneren over relaties en wiskundig onderbouwen dat hij wilde oproepen. Hij concludeert dat het zaak was deze opvattingen te veranderen. Het zou echter weinig zin hebben vergelijkbare opdrachten aan te bieden. De studenten zouden moeten worden uitgelokt om na te denken over de vraag waarom vermenigvuldigen hier de juiste aanpak is. Hij bedenkt dat de conceptuele problemen die hij in de les had waargenomen kunnen worden gebruikt om een cognitief conflict uit te lokken. Dit levert rechthoekenprobleem 2.

2 – Rechthoekenprobleem 2.
Bill zei, Als de tafel 13 rechthoeken lang is en 9 rechthoeken breed, en je telt eerst 1, 2, 3, …13 en dan 1, 2, 3…, 9 en vermenigvuldigt dan 13 x 9, dan heb je de rechthoek in de hoek twee keer geteld.’ Reageer op de opmerking van Bill.

Deze opgave leidt er inderdaad toe dat de studenten relaties gaan leggen tussen het tellen van de rechthoeken en het vermenigvuldigen van lengtes. De leerlingen geven aan dat het gaat om het tellen hoeveel er in een rij zitten, als je dan ook weet hoeveel rijen er zijn kun je die aantallen met elkaar vermenigvuldigen om het totale aantal rechthoeken te krijgen. Simon vraagt zich echter af of alle studenten hier wel echt over hebben nagedacht en niet domweg aanhaken bij wat er door anderen wordt gezegd. Wel heeft hij de indruk dat waar de redenering eerst zijnprobleem was nu het probleem van de studenten is geworden. Hoewel hij betwijfelt of dit voor alle studenten geldt. Bovendien is de context van de oppervlakte van een rechthoek wel een erg stereotype situatie en hij vraagt zich af of ze wel goed beseffen wat oppervlakte is. Hij besluit daarom een probleem te introduceren dat expliciet gericht is op het begrijpen wat oppervlakte is.    

3 – Het blob probleem.
Hoe kun je de oppervlakte van deze figuur bepalen?        

Dit levert de nodige discussie op. Uiteindelijk gaat de discussie over twee oplossingsmethoden. De ene is het idee dat je een touwtje om de blob zou kunnen leggen en dat touwtje vervolgens zou kunnen omvormen tot een rechthoek. De gedachte hierachter is dat als de omtrekken gelijk zijn, de oppervlaktes dat ook zijn. Deze veronderstelling wordt na enige discussie door de klas verworpen. Als tweede methode wordt voorgesteld om een plak deeg in de vorm van de blob te maken dat overal even dik is. Die zou je in kleine vierkantjes kunnen snijden. Van het deeg dat je overhoudt, kun je een nieuwe plak van dezelfde dikte maken waar je weer vierkantjes uit kunt snijden. Deze procedure kun je herhalen tot er te weinig deeg is om nog een vierkantje van te maken. De studenten zien in dat deze oplossing theoretisch wel O.K. is, maar moeilijk uitvoerbaar. Simon concludeert dat de studenten nu een goed besef hebben ontwikkeld van wat oppervlakte inhoudt en hij keert weer terug naar het oorspronkelijke probleem van de kartonnen rechthoeken op de tafel. 

Hij refereert nog eens aan het probleem van de gedraaide rechthoek, waarvan de studenten nu beseffen dat je daarmee niet het aantal rechthoeken krijgt dat op de tafel past. Simon vraagt nu of je met deze methode toch wel iets over de oppervlakte van de tafel kunt zeggen. De studenten zijn het er al snel over eens dat het getal dat je zo krijgt betekenisloos is als gevolg van de overlappende rechthoeken. Simon is hier nogal verbaasd over. Hij had gehoopt dat de studenten nu inzicht hadden gekregen in de relatie tussen het vermenigvuldigen van lengtes en oppervlakte. In eerdere cursussen leken de studenten te doorzien dat je vierkante oppervlakte-eenheden kon maken, waarvan de zijdes de lengte hadden van een kartonnen rechthoekje. Maar deze studenten leken echter zo overtuigd van de betekenisloosheid van de ‘omgekeerde-rechthoek procedure’ dat dit niet bij ze opkwam. Simon bedenkt daarom het volgende probleem.

4 – Het gedraaide rechthoekprobleem.
Buiten in de hal heb ik twee verschillende rechthoekige tafels. Daar heb ik deze methode gebruikt. Eerst heb rechthoeken in de ene richting afgepast. Daarna heb ik de rechthoek gedraaid en de andere zijde gemeten en de resultaten vermenigvuldigd. Op deze manier werkend kreeg ik bij tafel A 32 als uitkomst en bij tafel B 22. Mijn vraag is nu, is tafel A groter dan tafel B? Of is tafel B groter dan tafel A? Of heb je niet genoeg informatie om hier wat over te kunnen zeggen?

De studenten redeneerden dat, omdat 32 groter is dan 22, tafel A groter moest zijn. Op de vraag, ‘32 wat en 22 wat?’ antwoorden de studenten dat 32 en 22 niet naar betekenisvolle hoeveelheden verwijzen. Simon concludeert dat het niet is gelukt om de studenten aan het denken te zetten. Hij overlegt met een collega over de mogelijke oorzaak. Ze komen tot de conclusie, dat de studenten vast zitten aan het idee dat de kartonnen rechthoek de eenheid is waarmee je oppervlakte moet meten. Hij bedenkt een opgave waarin de kartonnenrechthoeken niet meer voorkomen maar lengtematen worden gebruikt.

5 – Het stokkenprobleem.
Twee mensen werkten samen om de oppervlakte van een rechthoekig gebied te bepalen. De een meet de lengte en de ander de breedte. Ze gebruiken elk een stok om mee te meten. Alleen de stokken die ze gebruiken zijn niet even lang. Louisa zegt, ‘de lengte is vier van mijn stokken’. Ruiz zegt, ‘de breedte is vijf van mijn stokken’. Wat weten ze nu over de oppervlakte van dit gebied?

Een van de studenten, Tony, betoogt dat het net zoiets is als meten met een rechthoek met een korte en een lange zijde. ‘Je krijgt dan 20 van zulke rechthoeken.’ Een ander merkt op dat ze het pas begreep toen Tony een tekening op het bord maakte. Dat je geen kant-en-klare oppervlaktemaat hebt, maar dat je die kunt maken. Door de ene stok als lengte en de andere stok als breedte van de rechthoekige eenheid op te vatten (figuur 9).

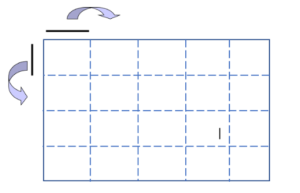
De meeste studenten beginnen nu de relatie te zien tussen de lineaire maten en de oppervlaktematen. Simon besluit nog een probleem met de gedraaide rechthoek aan te bieden om te kijken of dit inderdaad zo is.

6 – Gedraaide-rechthoek-probleem 2.
Ik gebruikte de kartonnen rechthoek en mijn methode (waarbij je de rechthoek draait) om twee rechthoekige gebied te meten. De ene was 3 x 4 en de ander 2 x 5. Teken deze gebieden op ware grootte en schrijf alles op wat je over de oppervlakte kunt vertellen.

De helft van de groepjes vond vierkanten waarmee je de oppervlaktes goed kon beschrijven.                                                                            

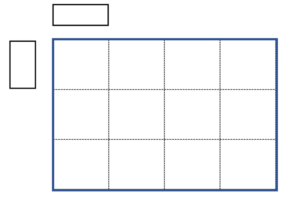
Zo rapporteert een groep dat ze eerst in beide richtingen rechthoeken hebben getekend – inclusief de overlap in de hoek. En daarna de overlap hebben weggehaald, omdat het om de lengte van de zijde gaat. In plaats van kartonnen rechthoeken kon je denken aan stokken, net als bij Louisa en Ruiz. En dan krijg je vierkanten als maat.

Een deel van de studenten die dit eerst niet gezien hadden begonnen in de loop van de discussie te begrijpen hoe het zat. Maar een aantal zag wel dat het werkte, maar vroeg zich toch af wanneer je nu rechthoeken moest gebruiken en wanneer vierkanten.

Samenvatting van de hypothetische leertrajecten en overwegingen

Terugblikkend merkt Simon op dat de opzet van de leergang start vanuit zijn eigen inzicht in de vermenigvuldigrelatie tussen de oppervlakte- en de lengtematen en de verwachting dat de studenten niet over dit inzicht beschikken. Ze kennen waarschijnlijk wel de regel maar zullen nooit diep hebben nagedacht over wat daarachter steekt. Dit maakte dit achterliggende inzicht een logisch doel voor de lessenserie. 

HLT 1. Hij koos daarom voor een activiteit waarin concreet gehandeld moest worden, om te vermijden dat de studenten direct met een formele oplossing zouden komen. Het werken met kartonnen rechthoekjes zou de studenten in de gelegenheid bieden om de formule af te leiden. Door de studenten slechts één rechthoekje per tafel te geven werd verder voorkomen dat de studenten het probleem tellend zouden oplossen. Uiteindelijk kwam één van de studenten (Molly) wel met de beoogde redenering maar de meeste studenten zagen het belang van zo’n redenering niet in.

HLT 2. Simon concludeerde dat het rechthoekenprobleem zijn probleem was gebleven en niet het probleem van de studenten was geworden. Hij deed daarom een nieuwe poging om een cognitief conflict op te roepen. Dit deed hij met de vraag of de rechthoek in de linkerbovenhoek niet twee keer wordt geteld. Dit ervoeren de studenten wel als een probleem dat om een oplossing vraagt en iedereen accepteerde ten slotte de redenering achter de vermenigvuldiging. Maar Simon had de indruk dat veel studenten zich passief aansloten bij anderen. 

HLT 3. Simon concludeerde dat de meeste studenten niet goed wisten wat oppervlakte inhoudt. Om daar wat aan te doen introduceerde hij het ‘blob probleem’. De studenten leken nu beter te beseffen wat oppervlakte inhoudt. Het feit dat de studenten met twee verschillende strategieën kwamen, stimuleerde hem om een aanvullende vraag te stellen, ‘Bij welke vormveranderingen blijft de oppervlakte gelijk?’ Een vraag die in feite ook nieuw was voor hemzelf. 

HLT 4. Nieuw voor hem was ook de noodzaak om dieper na te denken over wat je als oppervlaktemaat kiest als je niet uitgaat van een kant-en-klare oppervlaktemaat. Bij de tweede versie van het gedraaide rechthoekprobleem moest een oppervlaktemaat worden gevonden die bij dit probleem past. Dat zou een vierkant zijn waarvan de zijden gelijk zijn aan de lengte van de kartonnen rechthoek (figuur 10). Deze oplossing werd echter niet gevonden, de studenten bleken te gefixeerd op het kartonnen rechthoekje als oppervlaktemaat. 

HLT 5. Simon verving het meten met rechthoekjes daarom door meten met stokken (fig.8). Dit bleek te werken. 

HLT 6. Simon veronderstelde dat dit nu ook met de gedraaide-rechthoek zou lukken. Dit bleek inderdaad zo te zijn, de studenten begrepen dat je hier ook een nieuwe oppervlaktemaat kon creëren.

Tot slot

Achteraf, zou je kunnen zeggen dat het sneller had gekund. Wanneer Simon deze lessenserie nog eens geeft zal hij het stokkenprobleem vast eerder aanbieden. Maar het verslag is niet bedoeld om een optimale lessenserie te beschrijven, maar om een aanpak te beschrijven waarbij het actief construeren van kennis door de leerlingen/studenten centraal staat. Simon is trouw aan de inquiry gedachte. Uitgaande van wat hij op een bepaald moment over de kennis en inzichten van de studenten weet kiest hij zijn opdrachten. Die opdrachten kiest hij zo dat ze, (a) de studenten aan het denken zetten en (b) een volgende stap in het beoogde leerproces mogelijk maken. Steeds controleert hij of dit proces wel zo verloopt als beoogd en stuurt hij zo nodig bij. 

Al experimenterend, realiseert hij zich dat de eenheden waarmee je de zijden van de rechthoek meet, een bruikbare oppervlakte-eenheid opleveren. Het meten met stokken laat mooi zien hoe dit werkt. Daarbij kan worden opgemerkt dat je in feite in twee richtingen kunt denken, vanuit een gegeven oppervlakte-eenheid uitkomend op lengtematen, of startend met een lengtemaat uitkomend op een oppervlakte-maat. De formule ‘lengte keer breedte’ kan op eenzelfde manier worden begrepen. Bij het meten met standaardmaten kun je deze formule associëren met het afpassen van vierkantjes van 1 cm bij 1 cm, waarbij je op centimeters uitkomt als maat om de lengte en de breedte te meten. Of, omgekeerd, startend met het meten van de lengte en breedte van een rechthoek in centimeters, associëren met het tekenen en tellen van vierkantjes van 1 cm bij 1 cm.

literatuur

Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective.  Journal for research in mathematics education, 26(2), 114-145.