Een internationaal perspectief op reken- en wiskundeonderwijs, nr.6
In de internationale literatuur op het gebied van het reken- en wiskundeonderwijs staat het specifieke karakter van rekenen en wiskunde centraal. Deze literatuur laat zien dat dit vak heel specifieke eisen stelt aan het onderwijs. In deze reeks wil de werkgroep Wiskunde voor Morgen dit internationale perspectief voor het voetlicht brengen aan de hand van toonaangevende internationale artikelen.
Koeno Gravemeijer, Werkgroep Wiskunde voor Morgen
In deze bijdrage aan de serie worden drie artikelen van Paul Cobb en Erna Yackel besproken: Cobb, P., Yackel, E., & Wood, T. (1989), Cobb, P., & Yackel, E. (1996) en Yackel, E., & Cobb, P. (1996). De artikelen beschrijven een analysekader voor probleem-georiënteerd, interactief reken-wiskundeonderwijs. We zullen overigens, in navolging van de auteurs die spreken van ‘wiskunde’ (‘mathematics’), hier verder de term ‘wiskunde’ gebruiken, ook als het vanuit Nederlands perspectief, om rekenen gaat.
Cobb en Yackel bespreken in de genoemde artikelen het ontwikkelen van een model voor het analyseren van de interactie in de wiskundeles. Dit model – Cobb en Yackel noemen het een interpretative framework – wordt samengevat in figuur 1.

In het analysemodel worden twee perspectieven onderscheiden. Vanuit een sociaal perspectief wordt de ontwikkeling op groepsniveau geanalyseerd en vanuit een psychologisch perspectief de ontwikkeling van de individuele leerlingen. In het vervolg van deze bijdrage wordt uitgelegd wat de auteurs verstaan onder classroon social norms, sociomathematical norms en classroom mathematical practices.
Door de ontwikkeling van dit analysemodel is meer zicht ontstaan op de klassencultuur die voorwaardelijk is voor interactief, probleem-georiënteerd, wiskundeonderwijs en hoe deze tot stand kan worden gebracht. Cobb en Yackel gaan ervan uit dat leerlingen zelf wiskundige kennis en inzichten ontwikkelen door aan opgaven te werken die weliswaar binnen hun bereik liggen, maar waarvoor ze geen kant-en-klare oplossingsmethode hebben geleerd. Niet iedereen zal kiezen voor wiskundeonderwijs waarbij zo zwaar wordt ingezet op de construerende activiteit van leerlingen als Cobb en Yackel dat doen, maar het analysemodel is breder toepasbaar; je kunt er ook meer directieve onderwijsaanpakken mee analyseren en je kunt didactische aanpakken met elkaar vergelijken. Los daarvan zijn de inzichten die Cobb en Yackel ontwikkelen waardevol voor wie geïnteresseerd is in het vormgeven van interactief, probleem-georiënteerd, wiskundeonderwijs
Het uitgangspunt van beide onderzoekers is dat er – vanuit een constructivistisch perspectief – alleen sprake kan zijn van het leren van substantiële wiskunde als het leren het karakter heeft van problem solving. Met ‘problem solving’ wordt hier niet gedoeld op het oplossen van gangbare redactiesommen. Het gaat om de problemen die de leerlingen tegenkomen als ze proberen oplossingen te vinden voor opgaven die nieuw voor hen zijn. Die problemen kunnen allerlei vormen aannemen. Het kan zijn dat hun beschikbare kennis en procedures niet zomaar toepasbaar zijn in een nieuwe situatie. Het kan ook zijn dat ze te maken krijgen met een verrassend resultaat, of dat ze problemen ervaren wanneer ze proberen om hun manier van denken uit te leggen. Van de leerlingen wordt verwacht dat ze proberen om oplossingen te bedenken die passen bij hun actuele kennis en inzichten.
Classroom social norms
Centraal in de lessen staat het zelf bedenken van oplossingen, en het inbrengen van deze oplossingen in het klassengesprek. Hierbij gelden allerlei clasroom social norms, zoals Cobb en Yackel ze noemen, de sociale normen in de klas. Deze sociale normen, die vaak impliciet zijn, beschrijven hoe de lerares[1] en de leerlingen met elkaar omgaan. Cobb en Yackel wijzen erop dat een norm een gemeenschappelijke sociale constructie is. We kunnen dit illustreren met een voorbeeld (dat de auteurs overigens niet zelf gebruiken). Stel je de volgende situatie voor. Op straat vraagt iemand je, ‘Kun u mij zeggen hoe ik bij het Lindeplein kom?’ Nu weet je toevallig waar dat is en je zegt: ‘Hier rechtdoor, dan de eerste rechts, vervolgens de tweede links dan kom je bij het Lindeplein.’ De vragensteller antwoordt: ‘Hier rechtdoor, dan de eerste rechts, vervolgens de tweede links dan kom je bij het Lindeplein. Helemaal goed.’ En vervolgt met: ‘Kun je mij ook zeggen hoe ik in de Hoofdstraat kom?’ Je zou dat heel merkwaardig vinden. In de meeste klassen is zo’n soort gesprek echter heel gewoon. De lerares stelt vragen waar ze het antwoord al op weet. De leerlingen begrijpen dat het niet de bedoeling is dat ze zelf gaan nadenken, want het gaat om het antwoord dat de lerares in gedachten heeft. Dit is echter niet iets wat de lerares en de leerlingen samen hebben afgesproken. De leerlingen leren door ervaring wat de normen in de klas zijn, wat ze kunnen verwachten en wat er van hen verwacht wordt.
De auteurs benadrukken dat een sociale norm geen kenmerk is van een leerling, maar een gemeenschappelijke constructie. De lerares kan sociale normen niet opleggen. Wat zij wel kan doen is een proces van gemeenschappelijke sociale constructie initiëren en daar richting aan geven. De leerlingen hebben echter ook een rol. Zij dragen bij door in dit proces te participeren en door hun ideeën over hun eigen rol, en die van anderen, aan te passen. Er is echter geen causale relatie tussen de klassennormen en de individuele opvattingen van de leerlingen; er is alleen sprake van wederzijdse beïnvloeding.
De literatuur laat zien dat wat in een klas gebeurt op twee manieren kan worden geanalyseerd: vanuit een sociaal perspectief (waarbij je de groep als analyse-eenheid kiest) of vanuit een psychologisch perspectief (waarbij je een individu als analyse-eenheid kiest). Afhankelijk van wat je wilt weten. Cobb en Yackel gaan een stap verder, zij beschouwen de twee perspectieven als complementair. Wat betekent dat je beide tegelijkertijd in ogenschouw moet nemen.
Onderwijsexperiment
Het belang van de sociale normen komt naar voren bij een door de auteurs georganiseerd onderwijsexperiment in een Amerikaanse 2nd. grade classroom (onze groep 4). Al snel na de start van dit onderwijsexperiment blijkt de geplande onderwijsopzet van samenwerken in groepjes en klassendiscussies over inzichten en oplossingen niet van de grond te komen. De verwachting dat de leerlingen aan elkaar zouden uitleggen hoe ze de taken hadden geïnterpreteerd en opgelost, stond haaks op hun eerdere schoolervaringen. De leerlingen blijken ervan uit te gaan dat ze niet moeten proberen om zelf na te denken, maar dat ze de antwoorden moeten geven die de lerares in gedachten heeft. De lerares beseft dat er een groot verschil is tussen wat zij van de leerlingen verwacht en wat de leerlingen denken dat hun rol is. En ze besluit daarom met de leerlingen in gesprek te gaan over dit verschil in verwachtingen.
De gesprekken die de lerares met de leerlingen voert, worden door Cobb, Yackel en Wood (1989) aangeduid als, ‘renegotiation of classroom social norms’ (het heronderhandelen van de in de klas geldende sociale normen). De lerares stelt de normen die zij belangrijk vond expliciet aan de orde. Dit betreft met name:
- dat ze van de leerlingen verwacht dat ze hun oplossingen uitleggen en beredeneren,
- dat ze proberen om de oplossingen van andere leerlingen te begrijpen,
- dat ze aangeven of ze het met deze oplossingen eens zijn en
- dat ze de interpretaties of oplossingen waar ze het niet mee eens zijn ter discussie stellen.
De auteurs spreken in dit verband van obligations (verplichtingen) en expectations (verwachtingen). Deze verplichtingen en verwachtingen betreffen niet alleen de leerlingen maar ook de lerares. De leerlingen hebben niet alleen verplichtingen, maar ook ideeën over wat ze van de lerares mogen verwachten. Daar tegenover staan de verwachtingen die de lerares van de leerlingen heeft en de verplichtingen die ze ten aanzien van de leerlingen heeft.
Het woord ‘negotiation’ wordt gebruikt, omdat de lerares de nieuwe sociale normen niet zomaar kan opleggen. De term negotiation wordt hier echter wel op een specifieke manier gebruikt. Het is namelijk niet de bedoeling dat de leerlingen en lerares al onderhandelend uitkomen op andere sociale normen dan die welke de lerares vooraf al in gedachten had. De auteurs spreken van ‘onderhandeling’ om aan te geven dat de gespreksdeelnemers steeds moeten inspelen op wat de andere partij inbrengt. Zo zullen de leerlingen hun ideeën over wat hun verplichtingen zijn en wat ze van de lerares mogen verwachten, moeten bijstellen op basis van de wat de lerares zegt en doet. Omgekeerd is de lerares is afhankelijk van de inbreng van de leerlingen, want deze inbreng kan ze aangrijpen om duidelijk te maken wat ze belangrijk vindt. De posities zijn echter niet gelijkwaardig. De lerares kan haar autoriteit gebruiken om het onderhandelingsproces te sturen.
Om de manier waarop sociale normen veranderen te kunnen analyseren, maken de auteurs onderscheid tussen de normen op het niveau van de klas en de individuele opvattingen (beliefs) van de leerlingen. Kern hierbij is dat er sprake is van een voortdurende wisselwerking tussen deze twee. Enerzijds, worden de opvattingen van de leerlingen beïnvloed door de normen die zij in de klas ervaren. Anderzijds worden de normen van de klas als geheel beïnvloed door de persoonlijke opvattingen, die leerlingen in de discussie inbrengen. Cobb, Yackel en Wood (1989) illustreren dit proces met een aantal voorbeelden, waarin ze laten zien dat de emotionele gevoelens van de leerlingen een belangrijke rol spelen. Omdat Cobb en Yackel hun framewerk ontwikkelden tijdens werken in grade 2, onze groep 4, komen de voorbeelden in deze bijdrage uit dat leerjaar. Ze hebben het framework later ook in hogere leerjaren en in het voortgezet onderwijs toegepast.
Fouten maken
Een van de voorbeelden betreft Peter, die bij het uitleggen van zijn oplossing voor het bord, ontdekt dat hij een fout heeft gemaakt. Peter verontschuldigt zich en gaat snel terug naar zijn plaats. De lerares realiseert zich Peter zich geneert voor zijn fout en dat is nu net niet de bedoeling. Ze gebruikt deze situatie daarom om uit te leggen dat het geen probleem is als je antwoord fout blijkt. Ze benadrukt dat ze het veel belangrijker vindt dat de leerlingen nadenken:
That’s okay, Peter. It’s all right. Boys and girls, even if your answer is not correct, I am most interested in having you think. That’s the important part. We are not always going to get answers right, but we want to try.
De lerares laat hier zien hoe zij de situatie interpreteert. Ze laat blijken dat Peter zijn poging om het probleem op zijn eigen manier op te lossen, precies is wat de bedoeling is. Tegelijkertijd laat ze nog eens aan de klas zien dat het belangrijker is dat je wiskundig nadenkt dan dat je direct met het juiste antwoord komt.
In een vergelijkbare situatie vraagt ze aan een leerling – Jack – die een fout maakt: ‘Is it okay to make a mistake?’ Waarna ze nog eens toelicht dat het maken van fouten geen probleem is:
As long as you’re in my class it is okay to make a mistake. Because I make them all the time, and we learn from our mistakes, a lot. Jack already figured out, “Oops. I didn’t have the right answer the first time” (Jack turns and looks at the teacher and smiles), but he kept working at it and he got it.
Geleidelijk aan verandert de houding van de leerlingen. Het maken van fouten wordt niet meer beschouwd als iets waarvoor je je moet schamen, maar als iets wat er gewoon bij hoort.
Cobb en Yackel wijzen erop dat een implicatie van deze norm is dat de lerares zelf ook bepaalde verplichtingen moet accepteren voor haar eigen gedrag. Als ze van de leerlingen verwacht dat ze open zijn over hoe ze denken, dan moet ze de uitleg die ze geven ook accepteren zonder een oordeel over die juistheid te geven. Deze non-autoritaire, niet beoordelende rol bij het bespreken van de wiskundige oplossingen die de leerlingen naar voren brengen, staat in sterk contrast met haar sturende rol als het om de sociale klassennormen gaat. De auteurs gebruiken hier het onderscheid, talking about mathematics en talking about talking about mathematics. In het eerste geval stuurt ze niet in het tweede geval juist wel.
Doorzetten
Een andere sociale norm wordt door de lerares gecultiveerd door de leerlingen consequent te vragen om hun antwoorden toe te lichten. De leerlingen gaan hierop anticiperen en accepteren daarmee de verplichting om de opgaven zelf te doordenken. Dit stimuleert de leerlingen ook om door te zetten. In één geval heeft een groepje (Karin en Julie) zelfs 20 minuten aan een opgave gewerkt! Wanneer ze uiteindelijk de oplossing hebben gevonden wordt dit ervaren als een overwinning.
Teacher: How did you feel when you finally got your solution?
Kara and Julie: Good!
Het enthousiasme van beiden is goed zichtbaar, ze staan bijna te springen tijdens hun interactie met hun lerares. De lerares laat blijken dat deze leerlingen hun rol op de juiste wijze hebben opgepakt. Waarbij ze tegelijkertijd impliciet aangeeft dat het feit dat deze leerlingen zó lang nodig hadden gehad voor één opgave – terwijl anderen in dezelfde tijd meerdere opgaven hadden opgelost – niet moest leiden tot een gevoel van schaamte, of dom zijn. In plaats daarvan zijn gevoelens van trots en voldoening op zijn plaats wanneer je door doorzetten een persoonlijk uitdagende taak voor elkaar krijgt.
Voorzeggen
In deze sfeer past ook de norm dat de leerlingen geen antwoorden voorzeggen en niet voorgezegd willen worden. Zoals blijkt uit de volgende interactie:
Andy: Wow! I figured it out.
Teacher: What if someone asks you for the answer?
Andy: I won’t tell them.
Teacher: Good for you. Let them figure it out for themselves and get the enjoyment out of figuring it out for themselves. It makes us feel so good when we do something.
Wiskunde
Een belangrijk bijproduct is, dat de leerlingen gedurende dit proces van de ‘negotiation of classroom social norms’, ook specifieke opvattingen ontwikkelen over wat wiskunde is. In deze klas dient wiskunde uitlegbaar en verdedigbaar te zijn en gebaseerd te zijn op redeneren. Dat is wezenlijk anders dan wanneer je wiskunde ziet als abstracte, geobjectiveerde kennis die je op gezag van anderen moet accepteren. De rol van opvattingen over wat wiskunde is, wordt door Cobb en Yackel verder uitgewerkt is het concept, ‘socio-mathematical norms’.
Socio-mathematical norms
Yackel en Cobb (1996) merken op dat de classroom social norms heel algemeen zijn en niet specifiek zijn voor wiskunde. Ook bij andere vakken zul je immers willen dat de leerlingen zelf nadenken en hun inzichten verwoorden. Naast de algemene social normsintroduceren ze daarom ‘socio-mathematical norms’. Deze sociaal-wiskundige normen betreffen onder meer waardeoordelen over oplossingen. Zoals, bijvoorbeeld, of oplossingen wiskundig gezien verschillend, geavanceerd, efficiënt, of elegant zijn.Ook bij het oordeel of een gegeven uitleg of onderbouwing wiskundig acceptabel is, is sprake van een sociaal-wiskundige norm. Hier is de norm dat de uitleg gegeven wordt in termen van handelingen met wiskundige objecten.[2] Daarbij geldt bovendien, dat de uitleg door de andere leerlingen moet kunnen worden begrepen.
De auteurs geven enkele voorbeelden uit een (andere) 2nd-Grade klas.De leraar van deze klas, mr. K. vraagt regelmatig of iemand de opgave op een andere manier heeft opgelost. Er zijn echter vooraf geen criteria voorhanden op basis waarvan leerlingen kunnen bepalen wat als een ‘andere manier’ kan gelden. Of er wel of niet sprake is van verschillende oplossingen wordt pas duidelijk in de interactie tussen de leraar en de leerlingen. We zien hier eenzelfde proces als bij het ontwikkelen van de social norms. Enerzijds leren de leerlingen uit reacties de keraar welke oplossingen verschillend zijn, anderzijds is de inbreng van de leerlingen noodzakelijk als basis voor een reactie van de leraar.
Verschillende oplossingen
De eerste betreft de opgave: 16 + 14 + 8 = ….
Lemont vertelt dat hij eerst de eenheden van de eerste twee getallen bij elkaar heeft opgeteld. De twee tienen leveren samen 20, de 6 en de 4 nog een 10. Dat is 30 en nog 8 erbij is 38.Daarna komen een aantal oplossingen aan bod die veel op elkaar lijken. Allen gebaseerd op het splitsen van tientallen en eenheden, met kleine variaties in de volgorde waarin dat gebeurt. De leraar beoordeelt deze oplossingen als ‘bijna hetzelfde’. Dan komt er een leerling die 1 van de 16 heeft afgehaald en deze aan de 14 heeft toegevoegd. Dit levert 15 plus 15, waarvan zij weet dat het samen 30 is. Waarop de leraar reageert met een enthousiast ‘Yeah!’
Op deze manier leren de leerlingen dat het op verschillende manieren herstructureren van tientallen en eenheden als (wiskundig) verschillend wordt opgevat, maar het op een andere manier formuleren van een eerder gegeven oplossing niet.Het interessante is dat leerlingen op een geven moment zich ook gaan mengen in de discussie. Bijvoorbeeld, wanneer ze opmerken dat een nieuwe oplossing niet verschilt van wat eerder is verteld. De auteurs wijzen erop dat hier sprake is van een activiteit op een hoger cognitief niveau. Omdat de leerlingen twee oplossingen met elkaar moeten vergelijken, zijn de oplossingen zèlf nu onderwerp van reflectie geworden.
Efficiëntere oplossingen en oplossingen van een hoger niveau
Het leren onderscheiden van efficiëntere oplossingen of oplossingen van een hoger niveau, gaat subtieler in zijn werk. De leraar spreekt vrijwel nooit over een efficiëntere oplossing of een oplossing van een hoger niveau. Het zijn de reacties van de leraar waar de leerlingen uit moeten opmaken dat een bepaalde oplossing extra gewaardeerd wordt. Zoals de uitroep ‘Yeah!’.De leraar laat zijn waardering ook blijken, wanneer hij bij een opgave, expliciet om aandacht vraagt voor de oplossing van één van de leerlingen. De taak betreft een zogeheten ‘double-tens frame’ met vier rode chips in het linker ten-frame en zes rode chips in het rechter ten-frame (figuur 2).[3]
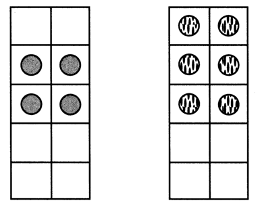
De ten-frames worden enkele keren kort getoond op de overheadprojector. Terwijl de leerlingen proberen te bedenken hoeveel chips er in het totaal zijn. Nadat een aantal leerlingen oplossingen hebben gegeven die allemaal gebruik maken van het tellen van eenheden, komt Travonda aan de beurt.
Travonda: You could say, um, um, it’s 6 on this side (pointing tot he right frame) [and] take one from that side and put it on the red side and …
Teacher: Listen to her!
Travonda: And [you] would have 5 plus 5.
Teacher: All right! Do you understand what she [said]. I like that! She said (pointing to the sceen) if we were to take one of these green and put it over here with, with the four [red chips] we’d have what?
Class: Five.
Teacher: Five. And this would leave five here (pointing tot he right tens-frame) and you could say 5 plus 5. That is good.
We kunnen dit beschouwen als een efficiënte oplossing, omdat je de chips niet één-voor-één hoeft te tellen. Maar de leraar vertelt niet aan wat er nu zo goed is aan deze oplossing, met zijn enthousiasme maakt hij wel duidelijk dat het hier om een bijzondere oplossing gaat. Het mooie is dat de leraar door deze manier van reageren aangeeft dat het hier om een meer geavanceerde oplossing gaat, terwijl hij de leerlingen de ruimte laat om wel of niet bij dit hogere niveau aan te haken. Een aantal leerlingen pakt de (impliciete) uitdaging aan om oplossingen te bedenken die ook bijzonder zijn.
Chad: You, you can put the four [red chips] on that [right] side and you would make10.
Teacher: Yeah! I like that.
Teacher: (To class) Chad says put these four (pointing to the red chips) over here (pointing to the blank spaces on the right frame) and that would make how many?
Class: Ten.
Teacher: Ten. Okay, that’s good. Yeah?
Greg: Two plus two is four (pointing to the red chips) and 2 plus 2 is 4 (pointing to four green chips) and that’s 8, and 2 more is 10.
Teacher: Right. Do you understand what he said? (The teacher repeats the solution for the class.)
John: You could do 7 plus 3 and then that would be 10.
Teacher: I like that.
Deze leerlingen blijken vrij snel op te pikken welk type oplossingen meer gewaardeerd wordt en komen met allerlei oplossingen, die het tellen overstijgen en nieuw zijn voor deze klas.
Ontwikkelingsonderzoek
De hier besproken onderzoeken zijn onderdeel van een reeks door Cobb en Yackel uitgevoerde ontwikkelingsonderzoeken. Om deze onderzoeken goed uit te kunnen voeren hadden ze een analyse-instrument nodig dat paste bij het beoogde onderwijs. Ontwikkelingsonderzoek omvat een reeks van cycli van ontwerpen en het onderzoeken van onderwijs. Zoals geïllustreerd in figuur 3.
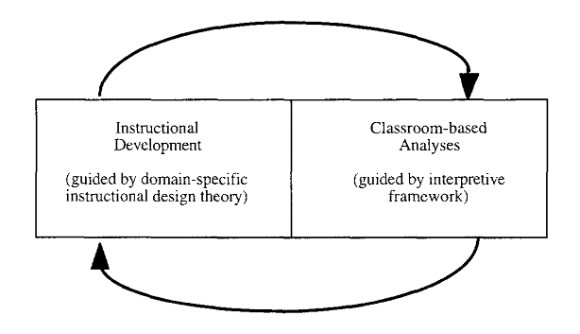
Het doel is te onderzoeken hoe je de gewenste vorm van leren van wiskunde kunt realiseren.
- De ontwerpkant van de cyclus omvat gedachte-experimenten, waarin wordt geanticipeerd hoe de leerlingen iets zouden kunnen leren – vergelijkbaar met de hypothetisch leertrajecten van Simon (1995).[4] De onderzoekers baseren zich hierbij op RME (wat staat voor, ‘realistic mathematics education’, in Nederland bekend als de realistische onderwijstheorie). Ze voegen daaraan toe dat ook rekening moet worden gehouden met de beoogde klassencultuur. De initiële ideeën over de te verwachten leerprocessen en over de manier waarop deze leerprocessen kunnen ondersteund, worden tijdens het onderwijsexperiment dagelijks beproefd en aangepast.
- Voor de analysekant van de cyclus is een interpretatiekader nodig dat zowel de wiskundige leerprocessen in beeld brengt, als ook de sociale context waarbinnen dit leren plaatsvindt.
De sociale context wordt in kaart gebracht door te kijken naar de sociale normen en de wiskundige normen enerzijds, en de individuele opvattingen van de leerlingen anderzijds. Hoe het wiskunde-leren zelf in kaart kan worden gebracht is echter minder vanzelfsprekend. Het hypothetisch leertraject is weliswaar een geschikt hulpmiddel om te anticiperen op de collectieve wiskundige ontwikkeling van de leerlingen als groep, maar voldoet niet als analyse-instrument. Het is namelijk niet aannemelijk dat alle leerlingen hetzelfde leertraject op dezelfde manier en in hetzelfde tempo zullen doorlopen.
Mathematical Practices
Omdat leerlingen een leertraject niet op dezelfde manier doorlopen maken Cobb en Yackel onderscheid tussen wat er op het klassenniveau gebeurt en wat er op het niveau van de individuele leerlingen gebeurt. De ontwikkeling op klassenniveau wordt opgevat als een opeenvolging van verschillende ‘mathematical practices’ (wiskundige praktijken). Deze mathematical practicesbeschrijven hoe een hypothetische leertraject in de praktijk van de klas uitpakt.
Op leerlingniveau wordt gekeken naar de manier waarop de leerlingen in deze wiskundige praktijken participeren. Het leren van een individuele leerling kan dan worden beschreven als een proces waarbij de manier waarop deze leerling in deze praktijken participeren verandert. Zo zien we ook hier weer een reflexieve relatie. De leerlingen leveren een actieve bijdrage aan de ontwikkeling van de wiskundige praktijken en omgekeerd leveren de wiskundige praktijken een stimulans voor de leerlingen om zich wiskundig te ontwikkelen.
De ontwikkeling van de wiskundige praktijk van het werken met tientallen als objecten
We kunnen dit toelichten met een voorbeeld uit een 2nd-Grade klas. In het begin van het schooljaar was het gebruik van allerlei tel-strategieën de gangbare praktijk. Een deel van de leerlingen was echter al verder. Zij waren inmiddels in staat om tientallen en eenheden als zelfstandige objecten op te vatten. Wanneer zij hier gebruik van maakten werden ze door de klas steeds gevraagd om hun oplossing uit te leggen. Later in het schooljaar werd dit type oplossingen door de klas vanzelfsprekend gevonden. Het interpreteren van getallen in termen van tientallen en eenheden is dan een gevestigde wiskundige praktijk geworden die niet meer hoeft te worden toegelicht. Dat getallen uiteengelegd kunnen worden in tientallen en eenheden wordt door de leerlingen ervaren als een wiskundig gegeven. Deze verandering voltrok zich in enkele weken.
Interpretative framework
Cobb en Yackel brengen de mathematical practices, samen met de social norms en de sociomathematical norms, onder in hun analysemodel, dat ze een interpretative framework noemen. We beelden het nogmaals af in figuur 4.

De analyse op klassenniveau richt zich op de sociale klassennormen, de sociaal-wiskundige normen en de wiskundige praktijken. De analyse op individueel niveau richt zich op de opvattingen, de wiskundige activiteiten en de inzichten van de individuele leerlingen. De auteurs benadrukken het belang van het coördineren van beide perspectieven. Het gaat uiteindelijk om de wisselwerking tussen wat er zich afspeelt op het niveau van de groep en wat er zich afspeelt op het niveau van de individuele leerlingen.[5]
Met dit interpretative framework kan geanalyseerd worden hoe het leren van wiskunde zich voltrekt in de context van de klassenpraktijk. De opeenvolgende wiskundige praktijken beschrijven de sociale situaties waarin de leerlingen wiskunde leren. De wiskundige activiteiten en wiskundige inzichten van de individuele leerlingen vormen daarbij de psychologische tegenhanger van de wiskundige praktijken. Het belang van het framework kunnen we illustreren met de constatering, dat uitspraken van leerlingen niet op waarde geschat kunnen worden wanneer je niet weet hoe de leerling zijn of haar rol ziet. Wanneer je niet weet of de leerling meent het door de lerares verwachtte antwoord te moeten geven of een eigen redenering.
Uiteraard zitten er inhoudelijke verschillen in de manieren waarop individuele leerlingen in een bepaalde wiskundige praktijk participeren. Het psychologische perspectief haalt deze verschillen naar voren. Terwijl het sociale perspectief de ontwikkeling op groepsniveau zichtbaar maakt.
De auteurs betogen dat het interpretative framework daarmee een krachtig instrument biedt voor het uitvoeren van ontwikkelingsonderzoek.[6] Ze plaatsen ontwikkelingsonderzoek daarbij tegenover klassiek onderwijsonderzoek, waar ze kritisch over zijn. Hun kritiek is dat de variabelen van experimenteel onderzoek tamelijk oppervlakkig zijn en weinig te maken hebben met context of betekenis, terwijl leerlingen altijd waarnemen, handelen, en leren door te participeren in een systeem dat groter is dan henzelf. Ze refereren hier aan wat Wenger (1998) een ‘community of practice’ noemt. In plaats van te veronderstellen dat alle leerlingen precies hetzelfde onderwijs krijgen, is het zinvoller om te analyseren hoe de leergangen in de praktijk worden vormgegeven. Dit is precies waar het hierboven beschreven interpretative framework voor is bedoeld.
Het creëren van een probleem-georiënteerde klassencultuur
De hiervoor beschreven voorbeelden[1] laten zien hoe het framework ook kan worden gebruikt om een klassencultuur te creëren die past bij interactief probleem-georiënteerd onderwijs. Kerninzicht is hier dat er continu sprake is van een wisselwerking tussen de normen op klassenniveau en de opvattingen van de individuele leerlingen. Nieuwe normen komen tot stand in een interactieproces, waarbij lerares en leerlingen steeds op elkaar reageren. De lerares gebruikt wat de leerlingen zeggen en doen, als concrete aanleiding om duidelijk te maken wat de gewenste normen zijn. Terwijl de leerlingen hun ideeën over wat de klassennormen zijn, aanpassen op basis van hoe de lerares op de oplossingen of opmerkingen van hen reageert.
Welke klassennormen een voorwaarde vormen voor interactief, probleem-georiënteerd wiskundeonderwijs zijn in het voorgaande geëxpliciteerd. Zoals, oplossingen uitleggen en beredeneren en proberen om de oplossingen van andere leerlingen te begrijpen. Ook de ‘socio-mathematical norms’, die nodig zijn voor het realiseren van de beoogde visie op wiskunde, zijn hierboven toegelicht. Deze betreffen onder meer de oplossingen en de onderbouwing ervan, die wiskundig van karakter moeten zijn en de normen voor het bepalen of oplossingen verschillend, geavanceerd, efficiënt, of elegant zijn.Cobb en Yackel laten in deze artikelen bovendien zien hoe deze normen in de praktijk tot stand kunnen komen.
Daarmee zijn de inzichten die de basis vormen voor het analyse-instrument niet alleen van belang voor onderzoekers, maar ook voor practici die een klassencultuur willen ontwikkelen waarin interactief, probleem-georiënteerd wiskundeonderwijs goed gedijt. Verder kan worden opgemerkt dat het analyse instrument niet alleen bruikbaar is voor het analyseren van probleemgericht interactief onderwijs. Ook het gangbare reken-wiskundeonderwijs kan ermee in kaart worden gebracht. Meer algemeen betekent dit dat dit instrument kan worden gebruikt om verschillende onderwijspraktijken met elkaar te vergelijken.
Literatuur
Cobb, P., Yackel, E., & Wood, T. (1989). Young children’s emotional acts while engaged in mathematical problem solving. In Affect and mathematical problem solving: A new perspective(pp. 117-148). New York, NY: Springer New York.
Cobb, P., & Yackel, E. (1996). Constructivist, emergent, and sociocultural perspectives in the context of developmental research. Educational psychologist, 31(3-4), 175-190.
Wenger, E. (1998). Communities of practice: learning, meaning, and identity, Cambridge University Press, 1998.
Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for research in mathematics education, 26(2), 114-145.
Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for research in mathematics education, 27(4), 458-477.
[1] Wanneer er in algemene zin naar leraren/leraressen wordt verwezen, gebruiken we ‘lerares’.
[2] Deze wiskundige objecten moeten ‘experientially real’ zijn voor de leerlingen. Dat wil zeggen dat ze onderdeel vormen van de wiskundige werkelijkheid van de leerling. Zie ook ‘Een internationaal perspectief op reken-wiskundeonderwijs 1 en 2’.
[3] Ten-frames worden gebruikt voor het rekenen onder de 20. Een ten-frame bestaat uit een afbeelding van 2 x 5 hokjes waar gekleurde chips in kunnen worden gelegd. Ze worden gebruikt voor tel- en rekenopdrachten, waarbij de structuur van de ten-frames het tellen en rekenen kan ondersteunen.
[4] Zie ook ‘Een internationaal perspectief op reken-wiskundeonderwijs nr. 4’.
[5] De auteurs laten ook zien dat het framework ook kan worden uitgebreid naar analyse eenheden als de school en de maatschappij waarbinnen het onderwijs wordt uitgevoerd. We gaan daar hier niet verder op in.
[6] Het belang van het framework kunnen we illustreren met de constatering, dat uitspraken van leerlingen niet op waarde geschat kunnen worden wanneer je niet weet hoe de leerling zijn of haar rol ziet. Wanneer je niet weet of de leerling meent het door de lerares verwachtte antwoord te moeten geven of een eigen redenering.
